ウエイトリフティング:バーベルの軌道の話
一時期流行った(まだ流行ってる?)バーベルの軌道ですが、一般の軌道のイメージは
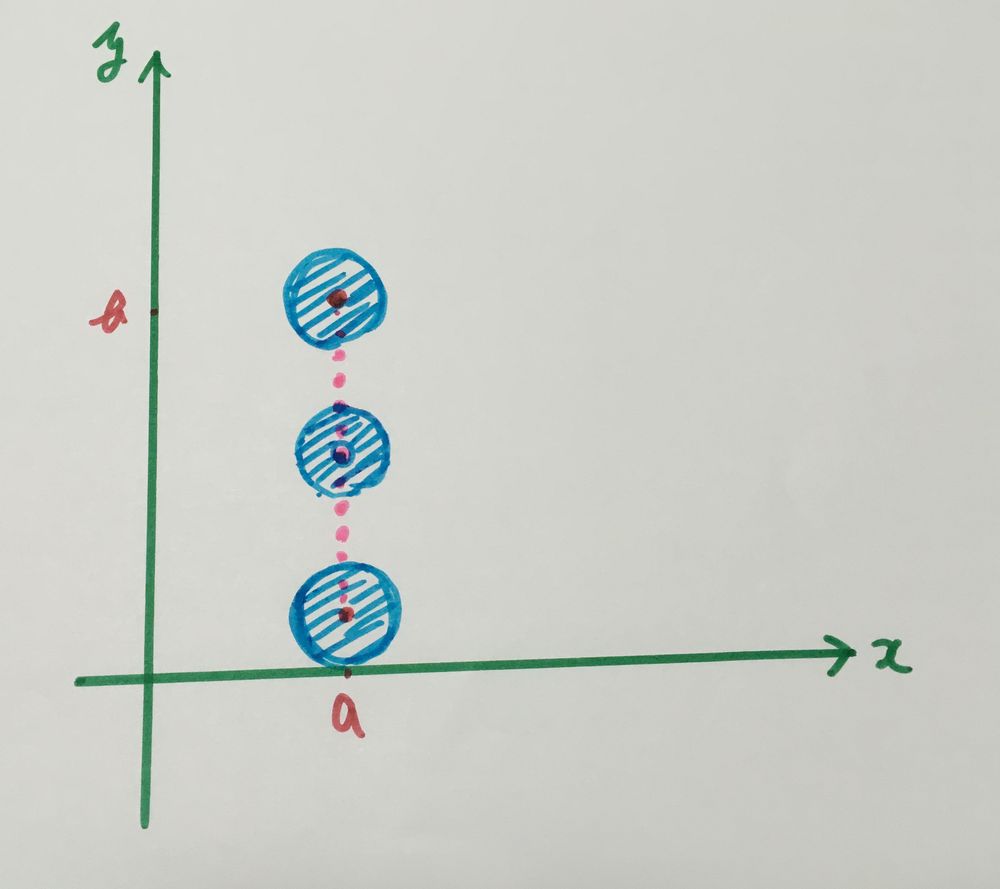
一直線で描ける。
しかし実際は
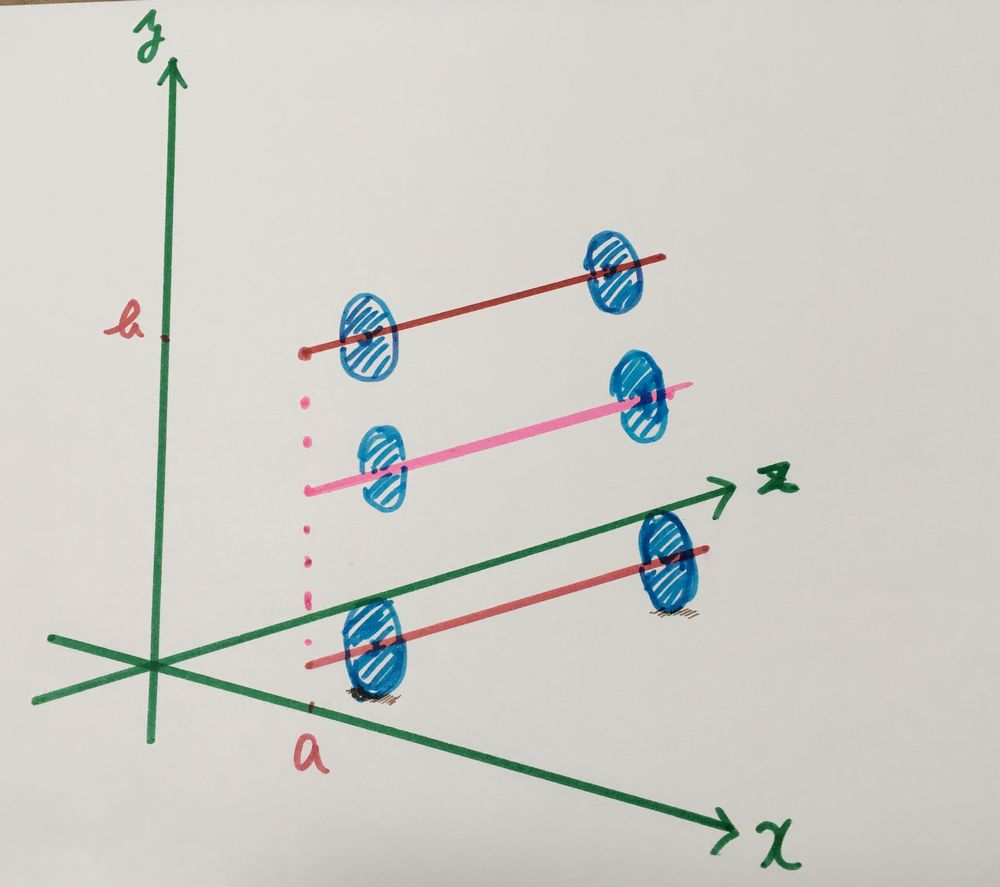
空間なのでバーベルは立体で捉えなければならない。三次元ですね。
XY平面から軌道を見てみると最初の画像と同じですが

直線で描けます。
しかし空間は三次元なので他の面からも見る必要があります。
ZY平面で見てみると
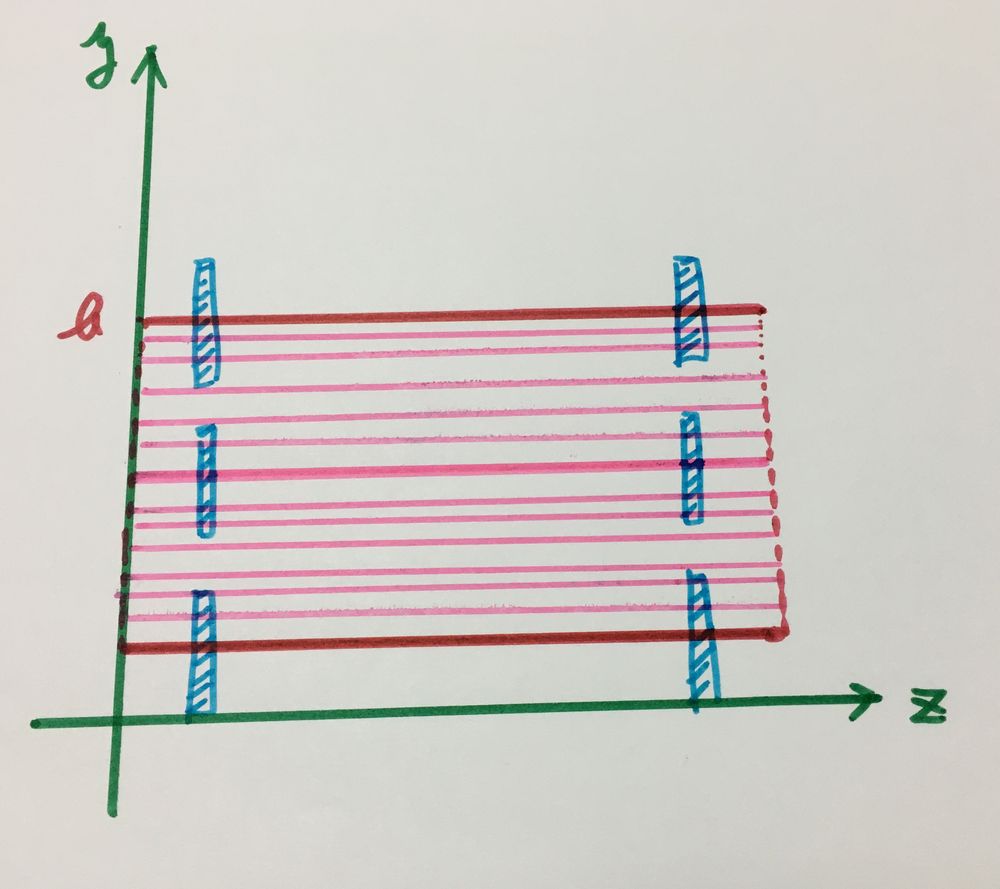
軌道はある意味直線ですが、イメージする直線とは違う感じ。
どちらかと言うと軌道は平面ですね。
では次にXZ平面で見ると
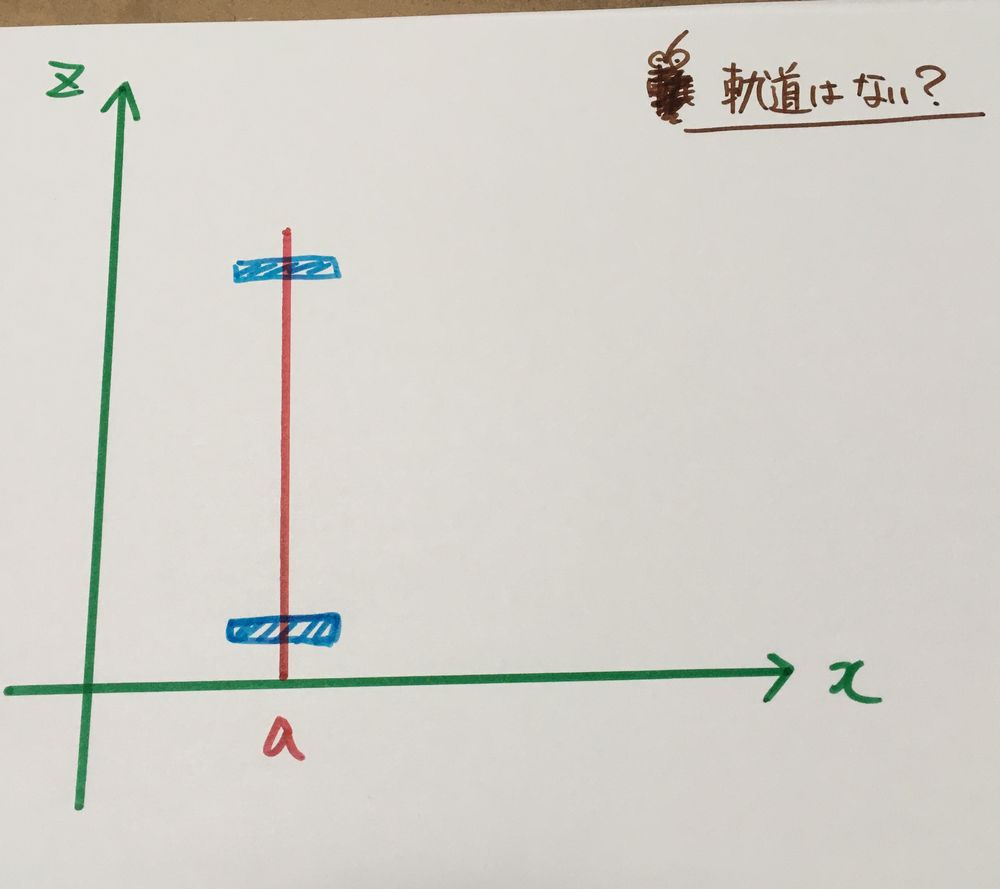
軌道の線は描かれません。
**********
線は点の集合体です。
バーベルを簡略化して記号化するとバーベルもまた直線で描け、そして点の集合体です。
バーベルの軌道ですので、バーベル上にある点はバーベルが動けはそれぞれ軌道を描きます。
それらはバーベル上のどの点の軌道も、バーベルの軌道なのです。
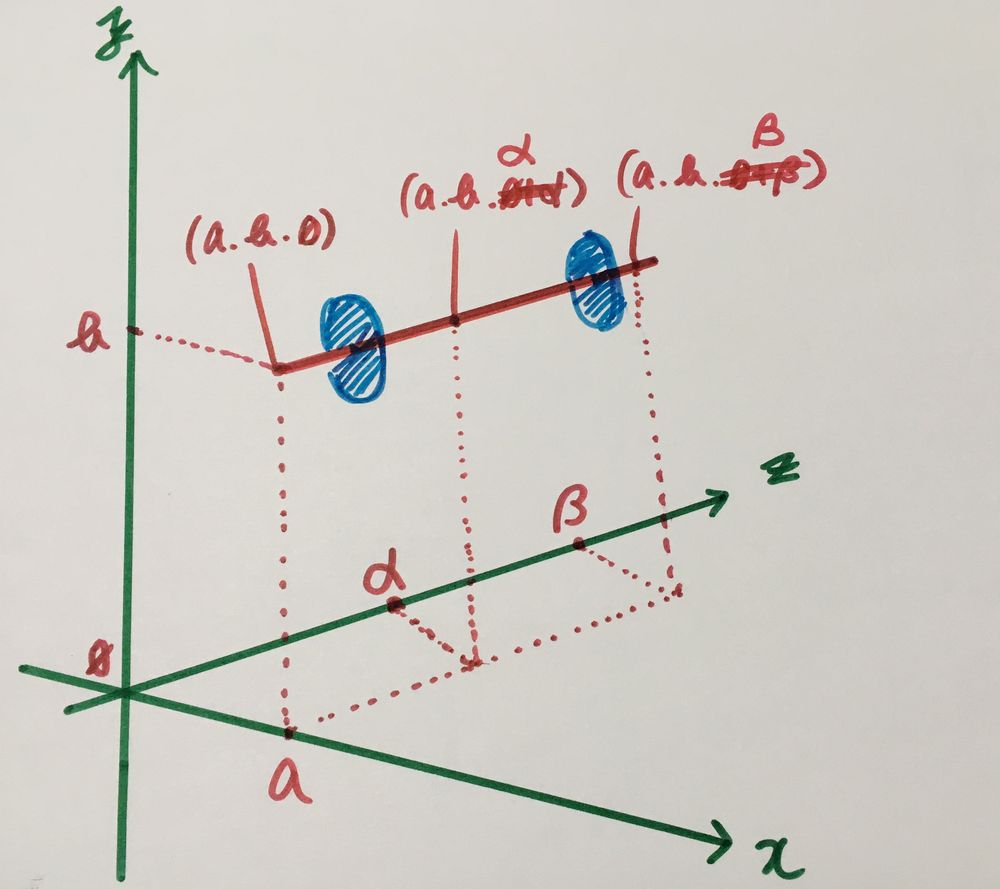
取りあえずこんな風に3点置きます。
この点がバーベルの軌道を描くということを理解しておいてください。
そして画像の図が適当なのは勘弁してください(本当に適当に描いているので)
では点をそれぞれXY、ZY、XZ3つの平面から見てみます。
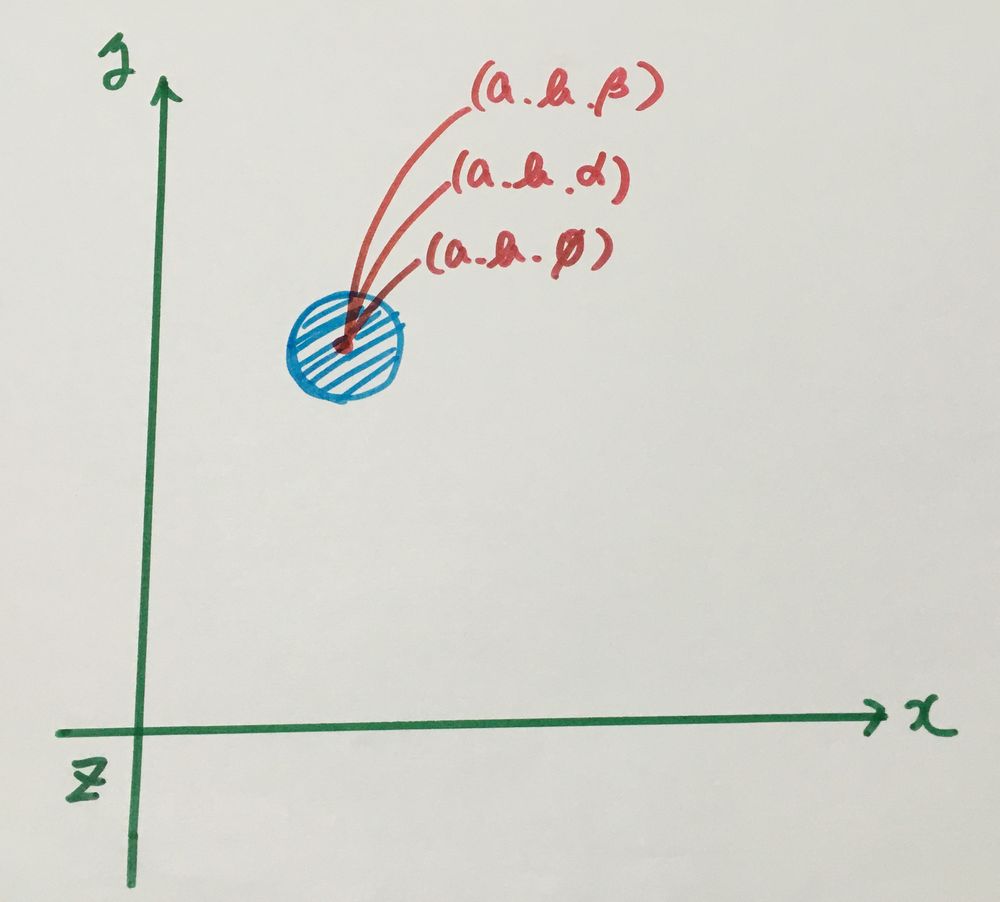
XY平面ではすべての点は1箇所に落ち着きます。
次はZY平面です。
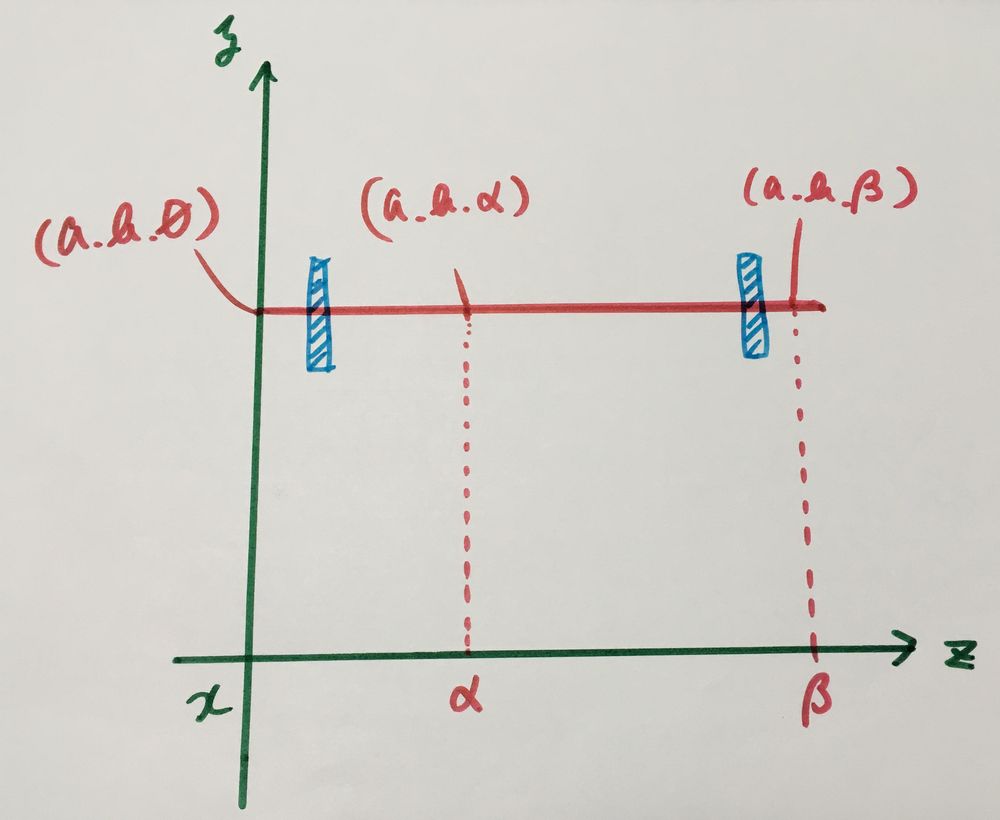
3つの点の存在が確認出来ると思います。
次はXZ平面。

こちらも点が3つあるのが確認出来ると思います。
さてここまでが前置きです。
尚、これは動画である程度解説してありますので、そちらも合わせてご覧いただけるとよろしいのではないかと思います。
次に続きます。
2020.6.10 新規

一直線で描ける。
しかし実際は

空間なのでバーベルは立体で捉えなければならない。三次元ですね。
XY平面から軌道を見てみると最初の画像と同じですが

直線で描けます。
しかし空間は三次元なので他の面からも見る必要があります。
ZY平面で見てみると

軌道はある意味直線ですが、イメージする直線とは違う感じ。
どちらかと言うと軌道は平面ですね。
では次にXZ平面で見ると

軌道の線は描かれません。
**********
線は点の集合体です。
バーベルを簡略化して記号化するとバーベルもまた直線で描け、そして点の集合体です。
バーベルの軌道ですので、バーベル上にある点はバーベルが動けはそれぞれ軌道を描きます。
それらはバーベル上のどの点の軌道も、バーベルの軌道なのです。

取りあえずこんな風に3点置きます。
この点がバーベルの軌道を描くということを理解しておいてください。
そして画像の図が適当なのは勘弁してください(本当に適当に描いているので)
では点をそれぞれXY、ZY、XZ3つの平面から見てみます。

XY平面ではすべての点は1箇所に落ち着きます。
次はZY平面です。

3つの点の存在が確認出来ると思います。
次はXZ平面。

こちらも点が3つあるのが確認出来ると思います。
さてここまでが前置きです。
尚、これは動画である程度解説してありますので、そちらも合わせてご覧いただけるとよろしいのではないかと思います。
- ⇒[youtube動画]ウエイトリフティング話Special~バーベルの軌道
- [youtube動画]ウエイトリフティング話Special~続・バーベルの軌道
- [youtube動画]ウエイトリフティング話Special~終・バーベルの軌道
次に続きます。
2020.6.10 新規